W nowym serwisie Zdzisława Dyrmy pojawił się link, który ma prowadzić to elitarnego forum. Chętnych do odwiedzin wita ciąg zadań do rozwiązania o rosnącym poziomie trudności. Zadania są generowane losowo, zatem nie można podpatrywać rozwiązań od kolegi z ławki ;) Przykładowy zestaw wygląda tak:
Trzeba przyznać, że pomysł jest całkiem sprytny. Odrobiny sprytu wymaga również pokonanie tego problemu w ciągu minuty – wystarczy znaleźć serwis w sieci, który takie całki rozwiązuje bez żadnego wysiłku. Trudno zatem uznać zabezpieczenie za skuteczne, bo instrukcja, jak je pokonać, może pojawić się za kilka minut w sieci.
Na deser zostawiamy najważniejszą część wiadomości – po rozwiązaniu ostatniej całki dalej nie dostaniecie dostępu do forum – bo forum na razie nie ma. Dostaniecie za to ciasteczko, które być może kiedyś może się przydać. O ile Zdzisław nie zmieni zdania.

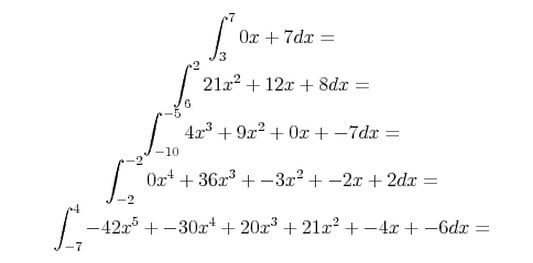



Komentarze
Pytanie tylko, czy Zdzisław mierzy czas potrzebny na rozwiązanie tych całeczek. Wtedy dość łatwo odgoni tych, co to lubią iść na łatwiznę :)
A jaka jest pewność, że ździsław znów się nie rozmyśli i nie będzie chciał sprzedać forum ? Jak dla mnie koleś stracił zaufanie w moich oczach.
Poziom trudności zadań ma sposób zachęcić użytkowników do łamania ich dlatego, bo podtekst tego jest „złamałeś zadanie jesteś debeściak i zasługujesz na moje forum”. W efekcie zakazany owoc najlepiej smakuje. Myślę, że to celowy zabieg.
Co to za nowa postać popkultury?
Dołączam się do pytania.
Wyniki
1. 7
2. 756 x^2+12 x+8
3. -x^3/25000+9 x^2-7
-x^3/25000+9 x^2-7
4. 36 x^3-3 x^2-2 x+2
5. -42 x^5-30 x^4+20 x^3+21 x^2-4 x-2407
To są całki oznaczone…
Widocznie kolega atom nie jest debeściak :)
Ale zadania są też na tyle proste, żeby studenci nie musieli zaglądać do ściąg ;).
@atom
Siadaj, dwója!
Od tego się przyda nasz żydowski kolega zza oceanu:
https://www.youtube.com/watch?v=ru7DK_BQidM
Brawo, jestes mistrz. Zdziszek jest z ciebie dumny. Nie kasuj ciasteczka, przyda sie na forum.
Bo wolfram alpha takie trudne
Trzeba przyznać że Zdzisio miał dobry pomysł z tym zadaniem ,wyobraźcie sobie youtube interie lub wp.pl gdzie zanim doda się komentarz należało by rowzwiązać całkę :) zapanował by błoga cisza :)))
i cofnęlibyśmy się do lat 90. Podziękuję.
Już wolę zadania ze spoja. Byłby większy odsiew.
@Stefan: Wystarczy nie czytać komentarzy :)
Zarzućcie ciasteczkiem
Wystarczyło by zadanie ile to jest 2+2 lub ile kończyn ma człowiek. 99% gimbo by odpadło…
Mógłby sobie jeszcze Zdzisław dołożyć nawiasy do tych całek, bo w tej formie to nie są poprawne matematycznie wyrażenia.
Niby czemu, wg mnie poprawne wyrażenie całkowe, chyba że chodzi ci znak dodawania i odejmowania obok siebie; dziwne, ale jednoznaczne
Poprawnie byłoby tak:
$\int_3^7 (0x+7)dx$
Ze strony Zdzisława: „Juz jest! Nowe forum.”